Stack based languages can be very powerful, but often can’t deal with arbitrary recursion. Andy Balaam finds a way around this limitation.
Some programming languages make recursive programming more practical by providing the tail call optimisation. For a lightning talk at the recent ACCU conference I looked at how we might do something similar in C++. This article attempts a fuller explanation.
| Tail call optimisation and the C++ standard | |
|
Multiplying by two
Here’s a toy problem we will use as our example.
Imagine for a second that you want to write a function that multiplies a number by two. OK, we can do that:
long times_two_hardware( long value )
{
return value * 2;
}
Now imagine that you don’t have the
*
operator.
We’re going have to use
+
. We can do that too:
long times_two_loop( long value )
{
long ret = 0;
for ( long i = 0; i < value; ++i )
{
ret += 2;
}
return ret;
}
(Obviously, this is just a silly example designed to be easy to follow.)
Now imagine that you read somewhere that state was bad, and you could always replace a loop with recursion. Then you might get something like this:
long times_two_naive_recursive( long value )
{
if ( value == 0 )
{
return 0;
}
else
{
return 2 + times_two_naive_recursive
(value - 1);
}
}
This is fine, but what happens when you run it for a large input?
$ ulimit -S -s 16 $ ./times_two naive_recursive 100000 Segmentation fault
Note that I set my stack size to be very small (16K) to make the point – actually, this will run successfully for very large arguments, but it will eat all your memory and take a long time to finish.
Why does this fail? Because every time you call a function, the state of the current function is saved, and new information is pushed onto the stack about the new function. When you call a function from within a function multiple times, the stack grows and grows, remembering the state all the way down to the place where you started.
So is programming like this useless in practice?
Tail call optimisation
No, because in several programming languages, the compiler or interpreter performs the ‘tail call optimisation’.
When you call a function from within some other code you normally need the state of the current code to be preserved. There is a special case where you don’t need it though, and this is called a tail call. A tail call is just the situation where you call a function and immediately return its return value as your return value. In this case we don’t need any of the state of the current code any more – we are just about to throw it away and return.
The tail call optimisation throws away this unneeded state before calling the new function, instead of after.
In practice, in compiled code, this involves popping all the local variables off the stack, pushing the new function parameters on, and
jmp
ing to the new function, instead of
call
ing it. This means that when we hit the
ret
at the end of the new function, we return to the original caller, instead of the location of the tail call.
Many recursive functions can be re-cast as tail-call versions (sometimes called iterative versions). The one we’re looking at is one of those, and Listing 1 is the tail-call version.
long times_two_recursive_impl( long total,
long counter )
{
if ( counter == 0 )
{
return total;
}
else
{
return times_two_recursive_impl(
total + 2, counter - 1 );
}
}
long times_two_recursive( long value )
{
return times_two_recursive_impl( 0, value );
}
|
| Listing 1 |
It consists of an outer function
times_two_recursive
which just hands off control to the inner function
times_two_recursive_impl
. The inner function uses a counter variable and calls itself recursively, reducing that counter by one each time, until it reaches zero, when it returns the total, which is increased by 2 each time.
The key feature of this implementation is that the recursive function
times_two_recursive_impl
uses a tail call to do the recursion: the value of calling itself is immediately returned, without reference to anything else in the function, even temporary variables.
So, let’s see what happens when we compile and run this:
$ ulimit -S -s 16 $ ./times_two recursive 100000 Segmentation fault
Did I mention that C++ doesn’t do the tail call optimisation?
So how would we write code that is tail call optimised in C++? Possibly of more interest to me personally: if we were generating C++ as the output format for some other language, what code might we generate for tail call optimised functions?
Tail call optimised C++
Let’s imagine for a second we have some classes, which I’ll define later.
FnPlusArgs
holds a function pointer and some arguments to be passed to it.
Answer
holds on to one of two things: either a
FnPlusArgs
to call later, or an actual answer (return value) for our function.
Now we can write our function like Listing 2.
Answer times_two_tail_call_impl( long acc,
long i )
{
if ( i == 0 )
{
// First argument true means we have finished -
// the answer is acc
return Answer( true, null_fn_plus_args, acc );
}
else
{
// First argument false means more work to do -
// call the supplied function with these args
return Answer(
false,
FnPlusArgs(
times_two_tail_call_impl,
acc + 2,
i - 1
),
0
);
}
}
long times_two_tail_call( long n )
{
return tail_call( Answer(
false,
FnPlusArgs( times_two_tail_call_impl,
0, n ),
0 ) );
}
|
| Listing 2 |
This has the same structure as
times_two_recursive
, if a little more verbose. The important point to note though, is that
times_two_tail_call_impl
doesn’t call itself recursively. Instead, it returns an
Answer
object, which is a delegate saying that we have more work to do: calling the provided function with the supplied arguments.
The trampoline
All we need now is some infrastructure to call this function, and deal with its return value, calling functions repeatedly until we have an answer. This function is called a ‘trampoline’, and you can sort of see why:
long trampoline( Answer answer )
{
while ( !answer.finished_ )
{
answer = answer.tail_call_();
}
return answer.value_;
}
While the answer we get back tells us we have more work to do, we call functions, and when we’re finished we return the answer.
Now all we need to get this working is the definition of
Answer
and
FnPlusArgs
, which are shown in Listing 3.
struct Answer;
typedef Answer (*impl_fn_type)( long, long );
struct FnPlusArgs
{
impl_fn_type fn_;
long arg1_;
long arg2_;
FnPlusArgs(
impl_fn_type fn,
long arg1,
long arg2
);
Answer operator()();
};
impl_fn_type null_fn = NULL;
FnPlusArgs null_fn_plus_args( null_fn, 0, 0 );
struct Answer
{
bool finished_;
FnPlusArgs tail_call_;
long value_;
Answer( bool finished,
FnPlusArgs tail_call, long value );
};
FnPlusArgs::FnPlusArgs(
impl_fn_type fn,
long arg1,
long arg2
)
: fn_( fn )
, arg1_( arg1 )
, arg2_( arg2 )
{
}
Answer FnPlusArgs::operator()()
{
return fn_( arg1_, arg2_ );
}
Answer::Answer( bool finished, FnPlusArgs tail_call, long value )
: finished_( finished )
, tail_call_( tail_call )
, value_( value )
{
}
|
| Listing 3 |
The only notable thing about this is that we use
operator()
on
FnPlusArgs
to call the function it holds.
Results
Now, when we run this code, we get what we wanted:
$ ulimit -S -s 16 $ ./times_two tail_call 100000 200000
(In other words, it doesn’t crash.)
So, it turns out that the tail call optimisation is just a
while
loop. Sort of.
Performance
You might well be interested in the performance of this code relative to normal recursion. The tail call version can process arbitrarily large input, but how much do you pay for that in terms of performance?
Recall that there are 4 different versions of our function, called
times_two
. The first, ‘hardware’, uses the
*
operator to multiply by 2. The second, ‘loop’ uses a for loop to add up lots of 2s until we get the answer. The third, ‘recursive’, uses a recursive function to add up 2s. The fourth, ‘tail_call’ is a reimplementation of ‘recursive’, with a manual version of the tail call optimisation.
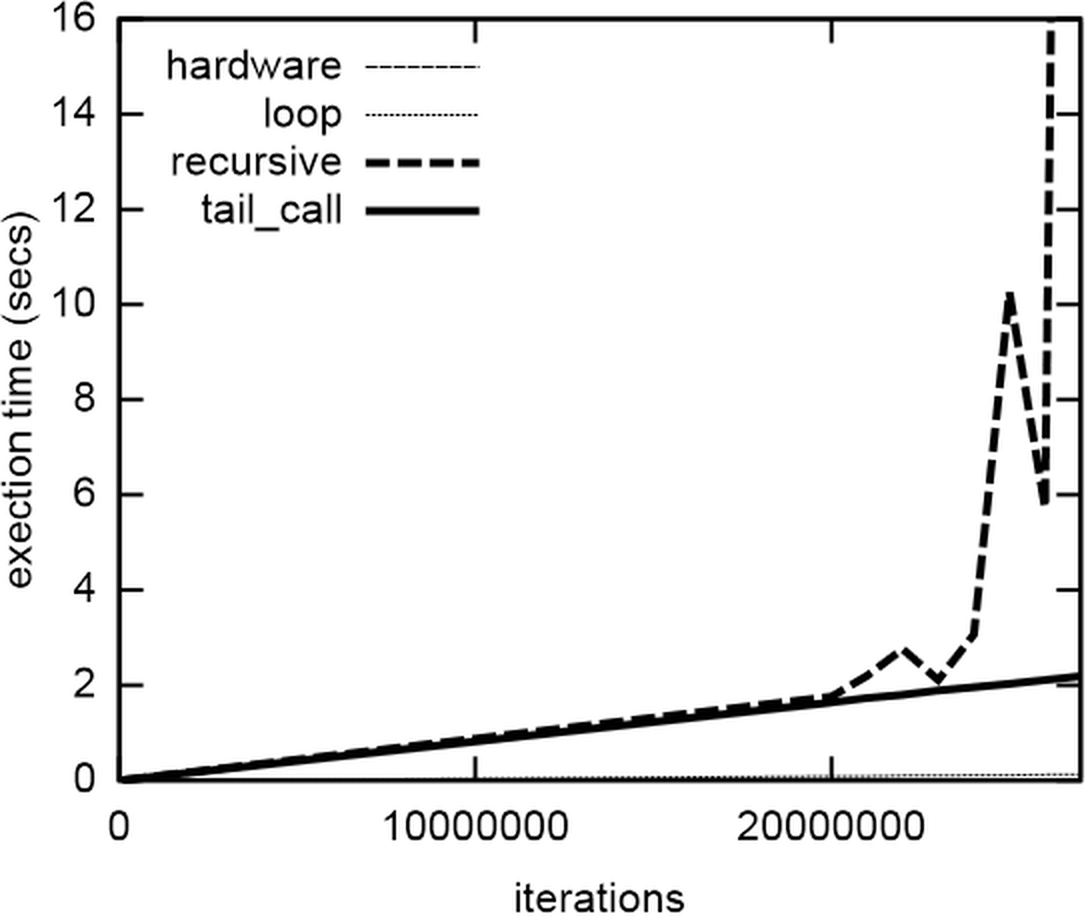
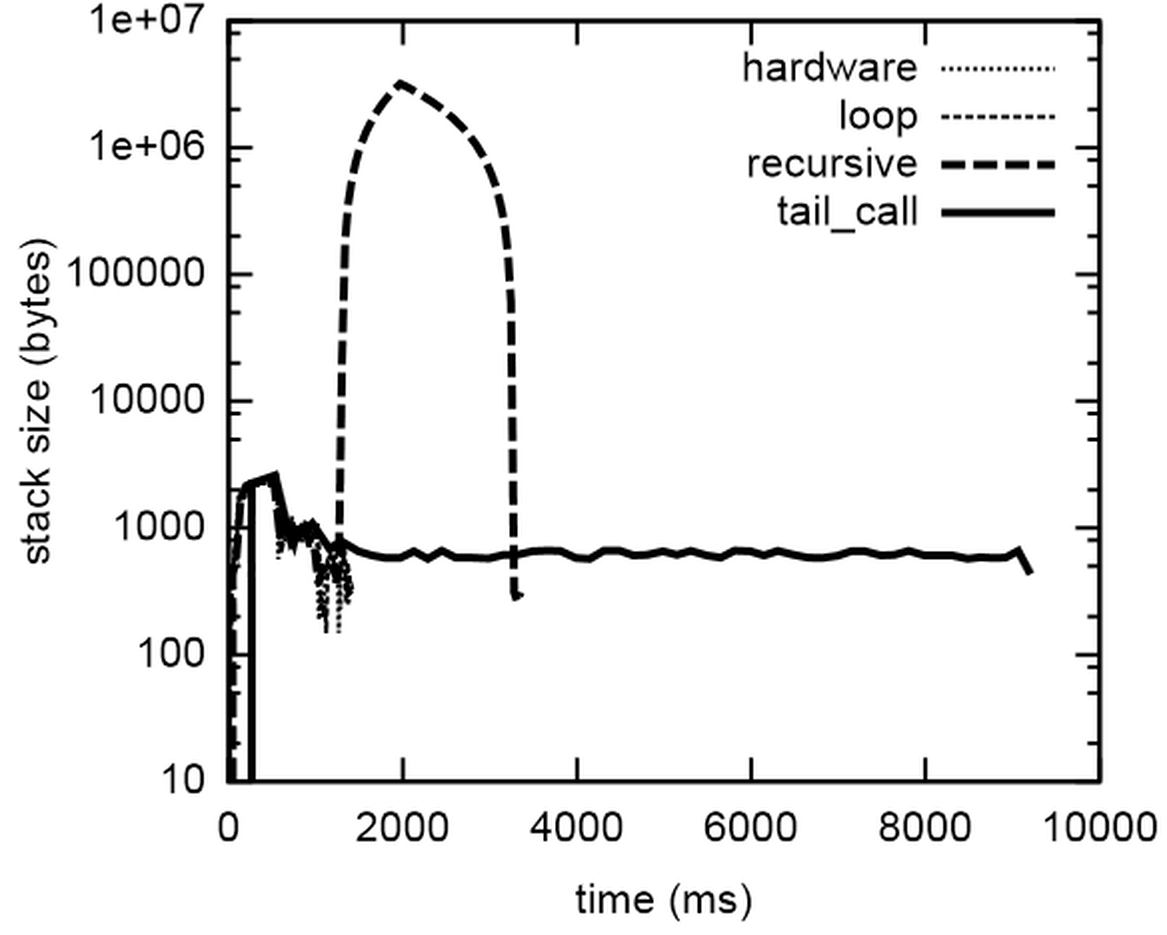
Let’s look first at memory usage. The stack memory usage over time as reported by Massif [ Massif ] of calling the four functions for a relatively small input value of 100000 is shown in Figure 1.
|
| Figure 1 |
The recursive function uses way more memory than the others (note the logarithmic scale), because it keeps all those stack frames, and the tail_call version takes much longer than the others (possibly because it puts more strain on Massif?), but keeps its memory usage low. Figure 2 shows how that affects its performance, for different sizes of input.
|
| Figure 2 |
For these much larger input values, the recursive and tail_call functions take similar amounts of time, until the recursive version starts using all the physical memory on my computer. At this point, its execution times become huge, and erratic, whereas the tail_call function plods on, working fine.
So the overhead of the infrastructure of the tail call doesn’t have much impact on execution time for large input values, but it's clear from the barely-visible thin dotted line at the bottom that using a for-loop with a mutable loop variable instead of function calls is way, way faster, with my compiler, on my computer, in C++. About 18 times faster, in fact.
And, just in case you were wondering: yes those pesky hardware engineers with their new-fangled
*
operator managed to defeat all comers with their unreasonable execution times of 0 seconds every time (to the nearest 10ms). I suppose that shows you something.
Generalisation
Of course, the code shown above is specific to a recursive function taking two long arguments and returning a long. However, the idea may be generalised. If we make our trampoline a function template, taking the return value as a template parameter, as in Listing 4
template<typename RetT>
const RetT trampoline_templ
( std::auto_ptr< IAnswer<RetT> > answer )
{
while( !answer->finished() )
{
answer = answer->tail_call()();
}
return answer->value();
}
|
| Listing 4 |
which must work with a pointer to an
IAnswer
class template like Listing 5
template<typename RetT>
struct IAnswer {
virtual bool finished() const = 0;
virtual
IFnPlusArgs<RetT>& tail_call() const = 0;
virtual RetT value() const = 0;
}
|
| Listing 5 |
which in turn uses an
IFnPlusArgs
class template (Listing 6)
template<typename RetT>
struct IFnPlusArgs {
typedef
std::auto_ptr< IAnswer<RetT> > AnswerPtr;
virtual AnswerPtr operator()() const = 0;
};
|
| Listing 6 |
we may generalise to functions taking different numbers of arguments, of different types. It is worth noting that only the return type is required as a template parameter. Concrete classes derived from
IAnswer
and
IFnPlusArgs
may be template classes themselves, but because of the use of these interfaces the types of the arguments need not leak into the trampoline code, meaning that multiple functions with different argument lists may call each other recursively. (Of course, they must all agree on the eventual return value type.) There is an example of how this might be implemented in my blog, along with the full source code for this article [
Code
].
Since this generalisation requires dynamic memory use (because the
IAnswer
instances are handled by pointer) this solution may be slower than the stack-only implementation above, but since all the memory is acquired and released in quick succession it is unlikely to trigger prohibitively expensive allocation and deallocation algorithms.
The examples [Code] demonstrate the use of template classes to provide
IAnswer
and
IFnPlusArgs
objects for each function type signature, and that functions with different signatures may call each other to co-operate to return a value. Generalising the supplied
Answer2
,
Answer3
etc. class templates to a single class template using C++11 variadic templates or template metaprogramming is left as an exercise for the reader.
References
[Code] http://www.artificialworlds.net/blog/2012/04/30/tail-call-optimisation-in-cpp/












